Engineers use oscilloscopes to capture data and make sense of it.  Modern scopes contain many tools that can be used for analyzing data, including Track and Trends, which graphically displays measurement results and locates anomalies. 

In addition, Tracks can synchronously demodulate a waveform which is useful for uncovering repeating characteristics within signals, while Trends are ideal for data logging, especially when characterizing slowly-changing phenomena.  The main similarity between Tracks and Trends is that the Y-axis of both operators is the measurement parameter itself (for example, pulse width, duty cycle, rise time, slew rate, etc.).  The main difference between the two math operators is their X-axis, in which the Track uses the identical X-axis and synchronous horizontal scaling as the input waveform.  An example of this is shown in Figure 1. 

Figure 1:  Pulse width modulated waveform (yellow) and track math operator (blue), where the X-axis scaling is identical for both.

Locating anomalies within a waveform is of great interest for design engineers, test engineers, and signal integrity engineers.  The Track provides valuable debugging information by directly pointing at the area of interest.  Notice that the negative-going spike in the Track waveform in Figure 1 occurs at the point in time where the input waveform reaches its most narrow pulse width, and the Track instantly finds it.  In this way, the Track acts as an anomaly-finding tool, indicating when one measurement deviates from the others in the graph.  The Track identifies the exact location in time where the narrowest or widest pulse width has occurred, and fully describes the measurement changes occurring throughout the entire waveform.   Since oscilloscopes can acquire thousands or even millions of waveform edges within a single acquisition, the Track allows an engineer to quickly "find the needle in a haystack."

In addition to locating anomalies, another use for the Track is to act as a demodulator.  When a repeating pattern occurs, the pattern is often not visible to the user because changes in the waveform are quite subtle relative to the repetition time. Consider the case of the same repeating pulse width modulation (PWM) pattern.  Shown in Figure 2, now the Track operator has demodulated a PWM waveform using a much longer time interval.  The shape of the pulse width modulation reveals a repeating modulation pattern which would not have been obvious to an engineer if not for the shape of the Track, because at the time scale needed to capture several repetitions of the PWM pattern, there are at least hundreds of pulse widths on the screen.   This allows for the user to identify which underlying data patterns exists within the data, and their rate of occurrence.

In order to determine how many pulse widths comprise one full repetition of a PWM pattern, the user can measure the frequency of the input waveform and the frequency of the pattern itself, and calculate the ratio of the two frequencies, as shown in Figure 2.  By graphing primary measurements, then demodulating the pulse train with the Track operator, secondary measurements on the Track provide a complete description of the underlying pulse width modulation scheme.   This type of application is where the Track math operator is at its best, where an engineer can combine math and measurement operators in a simple way to learn a great deal about the circuit's behavior.

Figure 2: Measurements on the Track waveform reveal that the modulation pattern repeats once every 45 cycles in this PWM waveform.

Could a Trend provide the same result as a Track?  To illustrate an important distinction between Tracks and Trends, the Trend math operator in Figure 3 is now applied to the same signal without reacquiring the input waveform.  Note that unlike a Track, the Trend is not time-synchronized to the input waveform and the timing of the underlying events is not retained. 

Instead of time, the Trend uses units of chronology for its X-axis.  Only the order of events, and not the timing of events, is retained.   The underlying shape of the Track may be displayed in the Trend because the same pulse width measurement values from a single acquisition are displayed in the same sequence. However, the timing information of when each of the pulses has occurred is not retained in the Trend.  Therefore, unlike the Track, the Trend does not point to the location of an anomaly.  Without time scaling, the Trend does not have frequency information needed to demodulate an input waveform.

Figure 3:  Applying the Trend operator to the same input waveform illustrates how (in contrast to a Track), the Trend operator is asynchronous to the input waveform.  

So far, we have only been focusing on the strengths of the Track.  Now it is time for the Trend to shine.  Figures 4 and 5 show an optimal application for the Trend operator.   Multiple waveforms are acquired, but only a single pulse is captured each time.  Figure 4 shows only a single pulse within the waveform record, but there are many values in the Trend.  Unlike the Track, the Trend can retain measurement results from previous acquisitions, which helps an engineer to retain a history of previous measurements compared with new measurements. 

Figure 4:  The Trend acts as a data logger when acquiring single pulses

The acquired pulse in Figure 5 is wider than the acquired pulse in Figure 4, and, therefore, it retains the full record of previous pulse widths and appends the new wider pulse value to the existing Trend, showing the history and evolving changes in the measurement.  The Trend allows for an engineer to observe long term changes due to timing drift across multiple acquisitions, which would not be visible in a Track.

Figure 5:  The most recent pulse width in the Trend was acquired seven seconds after the previous one.

When heating or cooling the device under test in a thermal chamber to test environmental effects, the Trend can show long-term variations in measurement values as the device temperature changes in the thermal chamber.  

Tracks are not ideal when there is a very low number of measurements per waveform. Shown in Figure 6, a Track and Trend are applied simultaneously to a single pulse. The Trend retains the history of pulses measured during previous acquisitions, allowing an engineer to determine how a device performs under varying operating conditions. By contrast, the Track operator is synchronized with the same time scale as the acquired pulse, and displays a flat line corresponding to the single pulse width which is overwritten with each subsequent acquisition.  Here a Track is not very useful and is used to illustrate why the Trend is optimal for this type of application.  

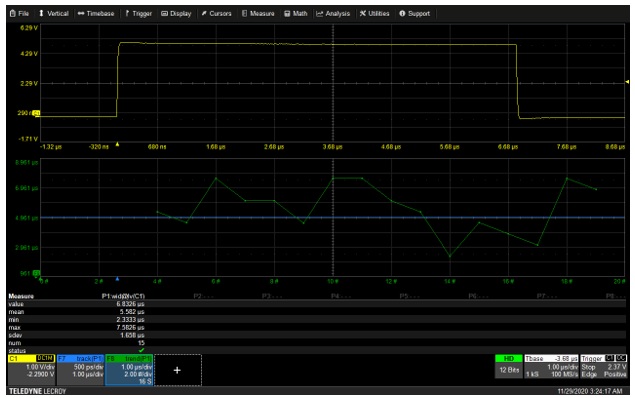
Figure 6: The Trend (green) retains a history of pulse widths, while the Track (blue) shows only a flat line corresponding to the most recent width.

Note that thus far, this discussion focused only on Tracking and Trending the pulse width measurement, in order to bring focus to the contrasts between the two math operators in this brief discussion, but Tracks and Trends can graph hundreds of other types of input measurement values, including rise time, fall time, duty cycle, skew, slew rate, setup and hold, custom scripted values, etc., which allows an engineer to characterize a nearly limitless set of varying circuit behavior.

As an example, Figure 7 is an example of trending DDR3 setup and hold times, timing between data and clock, and timing between data and strobe. Slow variations in timing measurements occur and are logged in the Trend, showing how timing changes as the device temperature increases.

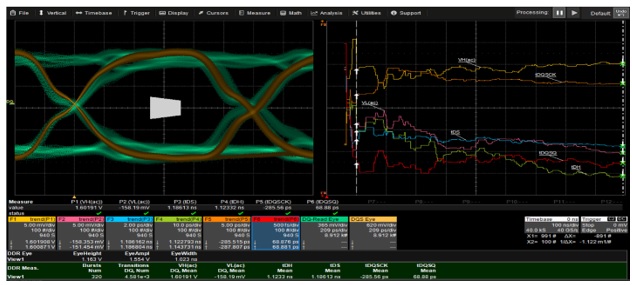
Figure 7:  Setup and hold times vary slowly over time as device temperature increases

By contrast, the Track will pinpoint where in time a specific problem occurs.  In the following real-world debug scenario, a clock cycle is intermittently dropped.  By using the Track, the exact location of the missing clock cycle is identified (see Figures 8 and 9).

Figure 8:  Tracking skew rate between clock and strobe shows spikes where anomalies occur.

Figure 9:  A spike in the Track waveform points to a missing clock cycle.

Both Track and Trend operators provide graphs of measurement results and identify anomalies.  Track operators incorporate the same horizontal scale as the source waveform of measurement, allowing the ability to demodulate a waveform and to pinpoint the exact locations of an anomaly, which is extremely valuable for correlation and cause-and-effect analysis.  Trend operators by contrast, are not synchronized to the input waveform, allowing the advantages of a reduced record size and the ability to retain the history of measurements that span across multiple acquisitions.  Depending on the applications needs and goals described above, either of these two operators can be the optimal choice.