Introduction

In getting the initial release of my PyChOpMarg Python package released recently¹, I had to go deep down the rabbit hole of COM, from specification to actual practice, aiming to resolve the differences in some way that made any engineering sense. The process left me battered, bruised, and shell shocked, a war torn soldier on the COM battlefield. I wrote this “field guide” in the hopes of helping others avoid the pitfalls I fell in.

What is COM?

The acronym “COM” stands for Channel Operating Margin.

The idea behind COM is to provide a means for qualifying channels for use at a certain bit rate and, perhaps, modulation and/or coding scheme, without requiring a full-blown serial link simulation and all the baggage that presumes. For example, things such as Tx/Rx IP models, trusted simulator, and talent able to drive the simulator and debug the models when they don’t cooperate. To that end, COM attempts to model “worst case” Tx and Rx analog termination and equalization schemes analytically, to gauge whether a particular channel design will support reliable information transfer according to a standard. The underlying thinking is: if your channel passes COM analysis, then it will work with any available Tx/Rx IP combination you might throw at it.

Clearly, the COM promise is an aggressive one. And the success it’s had is a testament to the caliber of engineering talent that created it. But, like all claimed panaceas, COM falls short in certain places. It’s important to be aware of where the chinks in its armor lie. This article attempts to provide a “field guide” for those working with COM, mapping out the pitfalls to avoid, and explaining the discrepancies between the specification and the MATLAB code, therefore guiding readers to a successful first experience with COM.

COM manifests in two primary forms:

• IEEE 802.3-22 Annex 93A: Annex 93A of the IEEE 802.3-22³ specification is the current normative standard for COM. It is written extremely well and the authors have been precise and efficient with their verbiage. What they are saying is perfectly clear. And, as far as I know, all their equations are correct.
• MATLAB Code: A body of M-code—the scripting language used in the popular MATLAB product sold and marketed by The Mathworks—has been written, ostensibly, to implement the equations found in Annex 93A of IEEE 802.3-22. It is this M-code that most COM practitioners are using to do their daily work in COM. My PyChOpMarg package is intended to give people a Python alternative to this M-code.

While the original intent of this M-code was to faithfully implement the equations in the standard, the code has become divergent from the standard in certain areas. It is important to understand where these differences lie and how to cope with them. I will attempt to explain these differences and will offer some suggestions on coping with them.

Why Do We Need COM?

So, why did we need COM? What motivated its creation?

There are really two answers to this question:

Channel Design Requires a “Worst Case” Tx/Rx EQ Definition

There needs to be a definition of “worst case” Tx/Rx termination and equalization, for any particular standard, such that channels for use with that standard may be designed independently of the Tx/Rx IP intended for the same standard. Without this standard definition of “worst case” IP, channels must be designed in conjunction with a particular Tx/Rx IP combination. This is very cumbersome. It’s much preferable to separate channel design from IP design, allowing them to proceed orthogonally.

The Reference for Qualifying Channels Should be Standardized

Before COM, we qualified our channels in conjunction with a particular Tx/Rx IP combination by running simulations of actual data moving through the channel/IP combination, either actually or “statistically.” The results of such simulations were then subjectively judged—presumably by someone with enough experience to have developed good judgement—to determine whether the channel would function adequately in production.

Withholding any objection to the subjective evaluation of engineering data for the time being, let’s just consider the combinatorial nature of this situation. We have as “variables” that might admit error into the process:

• The Tx model’s inaccuracy and how it differs between actual vs. statistical simulation runs
• The channel model, typically delivered in the form of Touchstone data and notoriously difficult to measure cleanly
• The Rx model’s inaccuracy and actual vs. statistical variability
• The tool-to-tool variability, with regard to simulation results produced for a particular Tx/Channel/Rx/simulation mode combination.

With a parameter space of this dimensionality and size, it can be very difficult to get true repeatability in channel qualification results.

Please note that the IBIS-AMI specification attempted to address this problem, by standardizing the way in which behavioral serial communication channel simulations were run, in both actual and statistical modes. However, success was partial at best. Different commercial tools, despite claims by their authors that they observed the standard, would routinely yield different results, given the same set of: Tx, Rx, channel, simulation mode, and operating parameters. (See Romi Mayder’s DesignCon2015 talk for an exposé of this.²)

The solution to this problem of repeatability is the standardization of an objective test procedure. This is exactly what COM has done. The authors of COM broke down the task of channel qualification into a series of well-defined steps, each with an algebraic equation specifying its correct implementation. They then fought to get those equations, along with their associated verbal explanations, accepted into the IEEE 802.3 (Ethernet) standard, for all the world to see and abide by, as Annex 93A.

How Do We Use COM?

So, how do we use COM to do channel qualification?

We really have two choices:

• IEEE 802.3-22 Annex 93A: Using the equations in Annex 93A of IEEE 802.3-22 as a guide, we can write code in our favorite numerical computing language implementing the COM algorithm. We can then run this code on our channel of interest and investigate the results. This is what I’ve done in creating my PyChOpMarg Python package.¹
• MATLAB Code: If we lack time and the ability to write our own code then we can make use of an M-code script, which has been made publicly available and purports to implement the COM specification. However, certain differences between more recent versions of this code and the specification have begun to appear. And these differences can cause the same sort of repeatability issues, as we’ve seen in the IBIS-AMI simulation arena, when results are compared to those of other scripts more adherent to the standard.

Current Differences

Here is a detailed list of those differences between v2.6 of the M-code and the standard, as given in IEEE 802.3-22 Annex 93A, which are known at the time of this writing:

• Crosstalk Calculation: The crosstalk calculation code was changed in 2018; that change marks a significant deviation from the standard
• ISI Calculation: The ISI calculator in the M-code includes pre-cursor positions, while the equation in the standard does not; it tallies only the post-cursor positions
• Cursor Location: When locating the correct cursor position, the M-code does not solve (93A-25) exactly, as the standard suggests, but rather minimizes the residual error in that equation.

Does COM Really Work?

If you’ve gotten this far then you’re probably considering taking the COM plunge and want to know: does it actually work?

Fortunately, the answer is: yes, it really does! However, there are some practical issues to be aware of.

Repeatability

Repeatability is the cornerstone of good “for production” engineering. No one wants to invest time in an approach that isn’t repeatable. So, is COM repeatable? Well, yes and no.

If you stick with the same version of the M-code—or of PyChOpMarg, or of your own implementation—and don’t change any of the operating parameters then, yes, it’s repeatable. But that’s obvious. The more interesting question is what happens when I attempt to compare results from PyChOpMarg, for instance, to results from a particular version of the M-code?

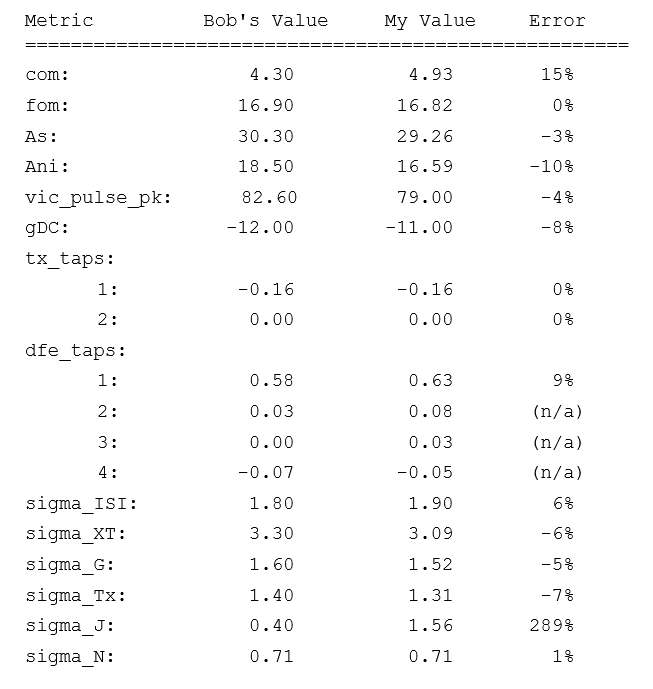
Here is an actual comparison of the results from those two tools, performed on one of the VITA¹  test channels:

As you can see, the agreement is quite good, but not excellent. The culprit seems to be my underestimation of the noise and interference term: Ani. The COM value is the ratio: As/Ani, expressed in dB.

So, what is the source of this discrepancy?

Spec. vs. Code

Looking at the various contributors to my underestimate for Ani (i.e. the “sigma_?” values at the bottom of the table above), it is clear that the sigma_XT term is the major culprit.

Note that, while the error in sigma_J is extreme, it is positive. We’re interested in negative errors, because we’re looking for causes of underestimation of Ani.

A perusal of that version of the M-code used to produce “Bob’s Results,” above, reveals the cause: the M-code has deviated from a true implementation of the specification.

Here are the pertinent equations, from the standard:

This is the original M-code:

The original code looks like a faithful implementation of equations (93A-33) and (93A-34).

However, here is the current M-code:

Clearly, the code has changed dramatically. For one thing, it is now doing something in the frequency domain. This is not the case with the original version. For another, it’s referencing equations (93A-46) and (93A-47), which come from a completely different section of the standard!

Worst Case

How about this assumption that COM represents a “worst case,” with regard to Tx/Rx equalization capabilities? Well, in general, it’s true. However, there is one glaring case where it is false:

What About Ideal DFE Assumption?

COM, in both its Figure of Merit (FOM) and noise and interference calculation phases, assumes an ideal DFE. That is, it assumes that the DFE will be able to perfectly cancel out all ISI in the system pulse response at each of the N post-cursor sampling locations, where N is the number of DFE taps, subject to any minimum/maximum bounds on its tap weights. Of course, no real world DFE will be able to achieve this because each possible sequence of symbols “pulls” the DFE tap weights towards a slightly different optimum setting. That’s why if you watch the DFE adaptation progress you will see it continuously “hunting” for the perfect solution.

Now, how can such an assumption of ideal DFE behavior lead to a “worst case” modeling of the Rx EQ? It can’t.

Conclusion

COM offers a simple and standardized way to perform channel qualification to a particular communication standard with the hope of repeatability. It is a very well written standard, in that it breaks the overall task down into nice bite-size and easily digestible chunks, each with an algebraic equation defining its correct implementation; about the best situation any implementer could hope for. Indeed, the normative definition of what COM is serves as an excellent reference of great specsmanship.

However, the current default implementation of the COM standard (the publicly available M-code) has taken such liberties, and become so divergent from the standard, that it defeats much of the standard’s excellent specsmanship, causing lack of repeatability.

Perhaps, the authors of the M-code might consider a rewrite in which any deviations from the letter of the standard must be explicitly requested, via command line options.

REFERENCES

1. D. Banas, "PyChOpMarg: Python Implementation of COM as per IEEE 802.3-22 Annex 93A," GitHub, 2024.
2. R. Mayder et al., "IBIS-AMI Model Simulations Over Six EDA Platforms," DesignCon, January 2015.
3. "IEEE Standard for Ethernet," IEEE Std 802.3-2022 (Revision of IEEE Std 802.3-2018), July 2022, doi: 10.1109/IEEESTD.2022.9844436.